Science behind Calcularis
Our History
Calcularis is a multi-sensory, computer-based learning program that has been developed by computer scientists at the Swiss Federal Institute of Technology Zurich (ETH Zurich) and neuropsychologists at the University of Zurich since 2010.
For almost 11 years more than 100.000 students tried Calcularis. We have been incorporating their learning experiences and findings into our software development process. Our computer scientists, educational professionals, PhD students and teachers - our main collaborators, are continuously working on optimising and enhancing content for Calcularis.
Our software represents an easy-to-use and mature tool, capable of adapting to many different learning scenarios. It provides individualised support for all students. It also makes it easier for teachers to support students, as all learning content, training history and progress are displayed in the Coach program.
Concept of Calcularis
Calcularis offers a new, unique way to support the brain during essential stages of learning and development. Our goal is to help brain automate basic skills, so that students could operate easily with basic math concepts.
How does our brain work?
The frontal lobe of the brain is associated with learning new skills, as it is involved in various cognitive processes such as reasoning, problem-solving, planning, decision-making, and working memory. These functions are crucial for acquiring new knowledge, adapting to novel situations, and mastering new skills.
In children, the frontal lobe is still developing and maturing. While some cognitive functions are present from early childhood, such as basic problem-solving and motor skills, higher-order cognitive abilities continue to develop throughout childhood and adolescence. So, when a child learns new skill or a new math concept, frontal lobes are activated.
The frontal lobe is used in understanding new mathematical principles, applying problem-solving strategies, and organizing information in working memory to perform calculations. Whereas the parietal lobe is involved in integration of sensory information and automation. In the context of basic math concepts, the parietal lobe contributes to tasks that require spatial reasoning, mental manipulation of numbers, and visualization of mathematical operations.
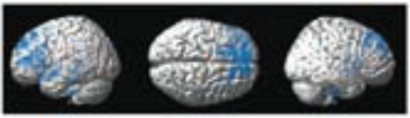
The frontal lobe is responsible for learning new concepts, logical thinking

The parietal lobe is responsible for automation and functional specialisation
Why is automation so important in math?
As children learn and practice basic math concepts, the frontal and parietal lobes work together to automate these skills. With repeated practice and reinforcement, the frontal lobe supports the acquisition of new mathematical knowledge and the development of efficient problem-solving strategies, and the parietal lobe facilitates the integration of sensory information and the execution of learned skills. As a result, basic math concepts become more automated and fluent, requiring less conscious effort to perform calculations accurately and efficiently.
As a result of automation, child can solve math problems more quickly and with less expenditure of effort. This ability of the brain to adapt to frequent tasks is referred to as brain «plasticity».
Specialisation of brain areas
Alongside the efficient automation of basic skills in math, Calcularis facilitates specialisation of individual brain regions.
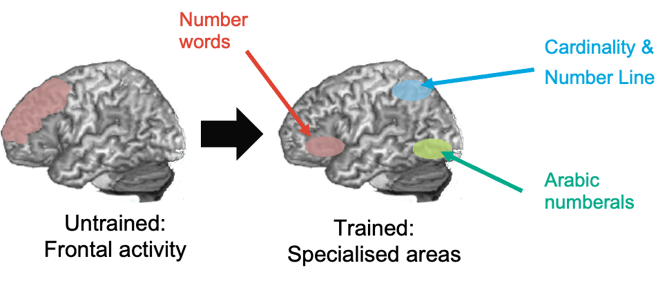
When we learn how to do math, various regions of the brain specialise particularly in the following tasks:
-
Processing of amounts (incl. estimation, comparison)
-
Number words (incl. retrieval of math facts)
-
Numerals and Arabic notation (incl. written tasks)
-
Concept of a number line (incl. estimating calculations, arithmetics)
In Calcularis, various game types are designed to simultaneously engage as many brain regions as possible by representing numbers as amounts, number words, Arabic numerals or positions on a number line. Calcularis also promotes the networking of these regions and the user‘s ability to switch between different forms of representation using:
-
Colors and animations
-
A 3D number line combining elements of the different forms
Thus, Calcularis makes it easier for the brain to specialise in basic skills and lays solid groundwork for freeing up capacity for more complex calculations.
Imagine asking a child this question: «What‘s eleven times ten?» If you present this question in the form of number words, students will likely be quick to picture the numbers 10 and 11 - that is, to convert to Arabic numerals. Some of them will do this automatically. Those who are experienced with mental arithmetic will be able to solve the problem easily by adding a 0 to the 11 - again, perhaps automatically. Their visualization of a number range will allow them to guesstimate that an answer of 110 is approximately correct.
